Slightly understating it, Dr. Iguaracy Pinheiro de Sousa knows a great deal about endothelial dysfunction. Apparently, because of this I entered in an algorithmic rabbit hole. It was a cool trip, overall.

In a conversation I had with him last year, he mentioned something about the cell type-specifc delivery of drugs injected in the bloodstream. As it is the case with many biotechnologies, the idea behind it is conceptually simple and techincally complex.

Bioactive molecules surrounded by lipid nanoparticles are one of the fanciest trends in drug development. Notably, some mRNA-based COVID-19 vaccines are also delivered in lipid nanoparticles (1). These drugs consist of molecules, that have a certain desired effect when inside the cells, surrounded by a tiny bubble of material that is similar to the membrane delimiting all human cells and their organells.

Such lipid shell isolates the molecules inside it from the environment, preventing their diffusion and degradation, and it also comes with another useful property: just like the cells’ membrane, it can host embedded proteins (2).

The tiny vescicles carrying the bioactive molecules can merge with the membrane of the cells. Upon fusion, the content of the vescicle is topologically destined to be found inside the cell that got it contact with the nanoparticle, in a process known as endocytosis. But which lipid nanoparticles merge with which cells doesn’t have to be random. In fact, depending on the proteins found on the two merging membranes, this event can have a high selectivity driven by receptor-ligand interactions.

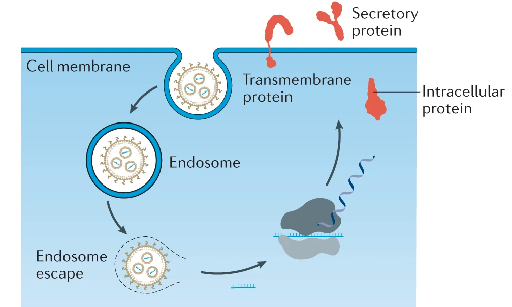
Schematic of a lipid nanoparticle–mRNA (LNP–mRNA) formulation entering the cell and delivering mRNA molecules that are being translated by the cell machinery, as in the case of mRNA-based COVID-19 vaccines. Adapted from (1).

Knowing this, the conceptually simple but technically complex next step is to engineer targeted endocytosis into the lipid nanoparticles, by embedding the right proteins to target the right cell populations, where the drug is intented to be delivered. Say, cells of a specific cancer that we want to kill. Or cells of a normal tissue in a normal organ that needs repair. Or that we want to genetically modify for metabolic or immunisation purposes.

Some researchers are already developing lentivirus-based platforms to display proteins of interest and deliver genetic cargo (3) to immune cells. While it is still far from being a routine approach in drug development, this kind of technologies will open up a vast landscape of therapeutic opportunities. I don’t think there are any theoretical hard constraits that would prevent us, in the future, from having a generic system to encapsulate arbitrary molecules into a vector displaying arbitrary (truncated) proteins on the outside.

These thoughts brought me to wonder further, and possibly too far. Imagining a platform like the one described above is established, we could deliver arbitrary molecular cargo specifically to cells in the body expressing a given combination of surface proteins. And we could do this with a simple injection. Having solved the manufacturing problem, selectively targeting the intended cell population among the vast atlas of human cell types will then just become a computational problem.

And here it’s where I stepped into the rabbit hole. Specifically, what is the smallest combination of membrane receptor proteins that uniquely identifies a cell population, distinguishing it from all other cells in the human body? Considering that almost 3,000 human proteins have been predicted to be potentially expressed in the membrane (4), and that in the Human Cell Altas over 1,900 cell types have been annotated (5) (whatever the definition of cell type should be … ), the answer is not immediately obvious.

This question is what prompted me to design and implement TrieSUS, as I wanted to find an efficient algorithm to solve the following problem:

Given a collection of sets, map each set to the smallest possible combination of its elements that uniquely identifies the set (here called a smallest unique subset, or SUS).

In this framework, if each set is a cell type, and the elements of the sets are the surface proteins expressed by the corresponding cell types, then the SUS of a set is the combination of proteins that we have to target to grant the cell type-specificity of drug delivery with our futuristic vector.

I was quite surprised not to find a name for this algorithmic question, since to me it seems quite a general one, so I decided to simply call it “the smallest unique subset” problem. Also, even though I wasn’t the first person on the Internet encountering this problem, I could only find brute-force approaches that involve enumerating the non-empty subsets of the set from the smallest to the largest (for example using the Gosper’s Hack) until finding one that is a solution, i.e. that is not a subset of any other set in the collection.

This approach, even taking some relatively obvious precautions such as making sure that potential solutions containing the least frequent elements in the collection are tested first, has exponential time complexity of O(2^n * m), where n is the number of elements in each set (assuming all sets have equal size) and m is the number of sets in the collection. In short, it scales very badly.

Somehow, I really couldn’t let the problem go, and I kept thinking about possible ways to solve it more quickly. Of course, this mostly happened at times when I was supposed to do something else. And of course, every time I realised I made a mistake and my algorithm wouldn’t return the optimal solution, I had the doubt that there was no real improvement to be found beyond the brute-force approach.

Eventually, after a lot of testing, simulated input, and trial and error, I came up with a program I’m quite satified of. TrieSUS implements a series of linear-time operations exploiting a trie-like data structure to first greatly reduce the problem size, and to then transform it into the equivalent of a set cover problem. The set cover is an NP-hard problem, but because of the reduced size of the input it will be treatable. TrieSUS then uses Google’s OR-Tools constrained programming solver to extract a solution. The result, as it can be seen from the figure below, is a great speedup, which could be especially important at the scale of the many cell subpopulation found in the healthy or diseased human body.

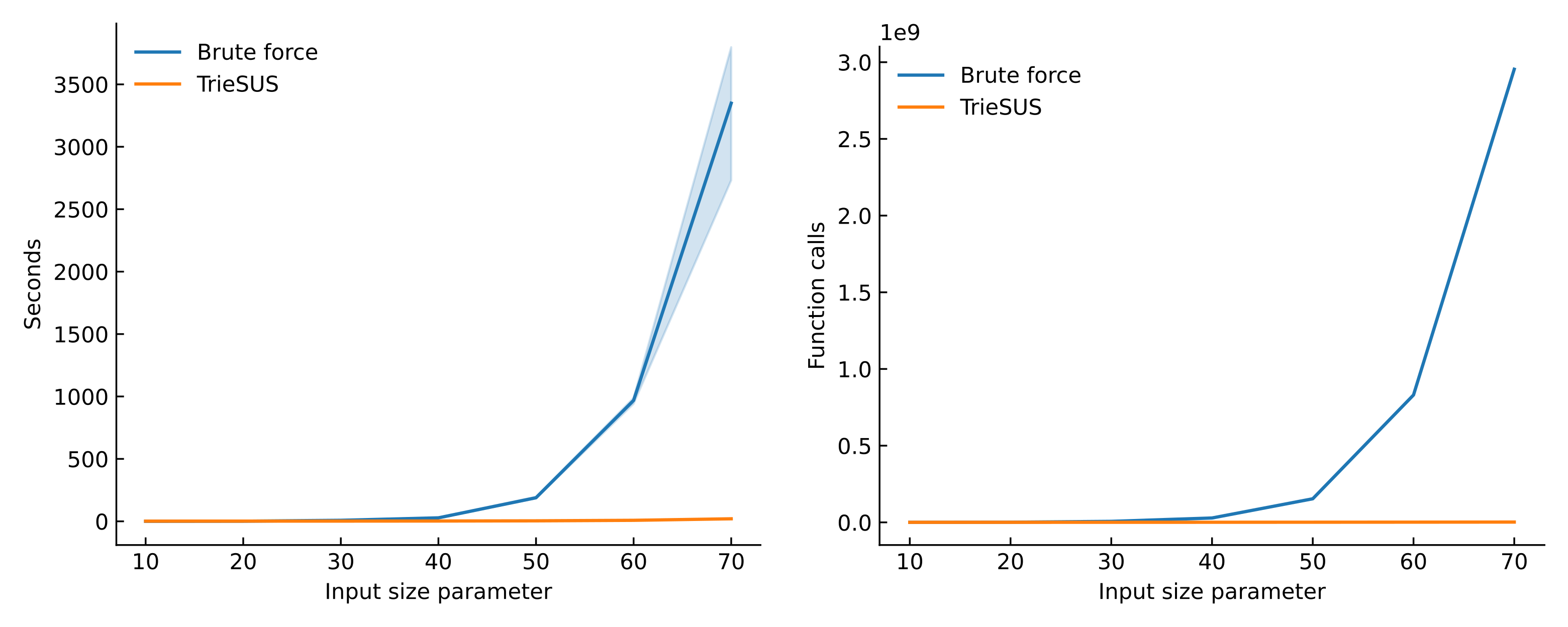
Performance of TrieSUS compared with the brute force baseline on randomly generated set collections. This analysis can be reproduced by cloning the TrieSUS benchmark repository. The input size parameter is a number corresponding to three quantities: the number of sets in the collection, the number of items in the universe, and the maximum number of items in each set.

More details about TrieSUS and its implementation can be found in the GitHub repository.

References

1. Hou, X., Zaks, T., Langer, R. et al. Lipid nanoparticles for mRNA delivery. Nat Rev Mater (2021). https://doi.org/10.1038/s41578-021-00358-0
2. Frauenfeld, J., Löving, R., Armache, JP. et al. A saposin-lipoprotein nanoparticle system for membrane proteins. Nat Methods (2016). https://doi.org/10.1038/nmeth.3801
3. Yu, B., Shi, Q., Belk, J. A. et al. Engineered cell entry links receptor biology with single-cell genomics. Cell (2022). https://doi.org/10.1016/j.cell.2022.11.016
4. Bausch-Fluck, D., Goldmann, U., Müller, S. et al. The in silico human surfaceome. PNAS (2018). https://doi.org/10.1073/pnas.1808790115
5. Osumi-Sutherland, D., Xu, C., Keays, M. et al. Cell type ontologies of the Human Cell Atlas. Nat Cell Biol (2021). https://doi.org/10.1038/s41556-021-00787-7